一、内参与外参概念
在计算机视觉中，特别是在相机标定和立体视觉领域，内参（Intrinsic Parameters）和外参（Extrinsic Parameters）是非常重要的概念。它们与相机的几何属性和姿态有关。
内参（Intrinsic Parameters）： 内参是描述相机内部属性的参数，包括焦距、主点（光学中心）坐标、畸变系数等。内参通常在相机标定时确定，因为它们通常对于特定相机型号是固定的，不随时间变化。一旦相机内参被确定，它们在相机的使用过程中通常是保持不变的。
外参（Extrinsic Parameters）： 外参是描述相机在世界坐标系中的位置和姿态的参数，通常包括旋转矩阵和平移向量。外参在不同的相机位置或拍摄时刻可能会发生变化。例如，在立体视觉中，如果有两个相机，那么它们的相对位置和方向会在每次移动相机时发生变化，从而导致外参的变化。如果相机不发生位置和方向的变化，比如相机固定在一个固定位置，那么外参在很长一段时间内可能保持不变。然而，如果相机的位置或方向发生变化，例如移动相机或更改拍摄角度，外参会随之变化。
二、四个坐标系
四个坐标系的意义，世界坐标系（参考坐标系）、摄像机坐标系、图像物理坐标系和像素坐标系。
世界坐标系就是物体在真实世界中的坐标，比如黑白棋盘格的世界坐标系原点定在个棋盘格的顶点，，，互相垂直，方向就是垂直于棋盘格面板的方向。可见世界坐标系是随着物体的大小和位置变化的，单位是长度单位。只要棋盘格的大小决定了，无论板子怎么动，棋盘格角点坐标一般就不再变动(因为是相对于世界坐标系原点的位置不变)，且认为是。
相机坐标系以光心为原点，以平行于图像的和方向为轴和轴，轴和光轴平行，，，互相垂直，单位是长度单位。
图像物理坐标系以主光轴和图像平面交点为坐标原点(一般为图像中心)，和方向如图所示，单位是长度单位。
图像像素坐标系以图像的左上顶点为坐标原点，和方向平行于和方向，单位是以像素计。
相机成像过程一般涉及到四个坐标系的变换，变换关系为：是世界坐标系，经过刚体变换（如：旋转、平移）后变为了相机坐标系，再次经过透视投影转变为了图像坐标系，最后经仿射变换转换为了像素坐标系。
我们考虑最简单的小孔成像模型：
为了分析的方便，经常将成像平面沿小孔（光心）对称处理，使图像不再倒立，如图中蓝色实线所指平面。
三、相机外参
外参矩阵是世界坐标系到相机坐标系的变换。既然是变换，我们就能够将其表达为[R t],齐次形式为
但是目前为止好像并没有在相机矩阵中看到外参矩阵。之前的相机矩阵表示如下：
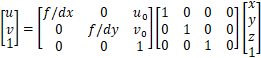
那是因为，之前的推导中，我们默认世界坐标系和相机坐标系是重合的。在小孔成像模型中，空间一点的坐标被描述为[x y z 1]，这个点的坐标系原点在小孔，而相机的坐标中心也在小孔，但是在实际应用过程中，世界坐标系和相机坐标系往往不重合，这样才带来了外参矩阵的概念，下图展示了相机坐标系与世界坐标系不重合时的情况，我们只知道P点在世界坐标系下的坐标，因为要运用小孔成像原理，我们想知道P点在相机坐标系下的坐标，相机外参矩阵就实现了这种变换。
还是空间某个点p，其在世界坐标系下表示为[xw,yw,zw,1]，在相机坐标系下表示为[xc,yc,zc,1]，那么它们具有如下关系：
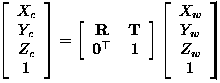
带入到相机矩阵表达式中可以得：
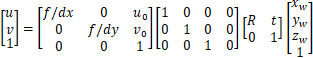
合并等式右边2、3两个矩阵：
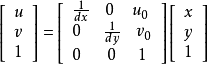
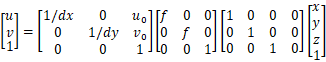
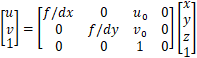
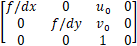
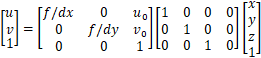
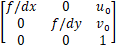称为内参矩阵（少了一列0），都是一个意思。